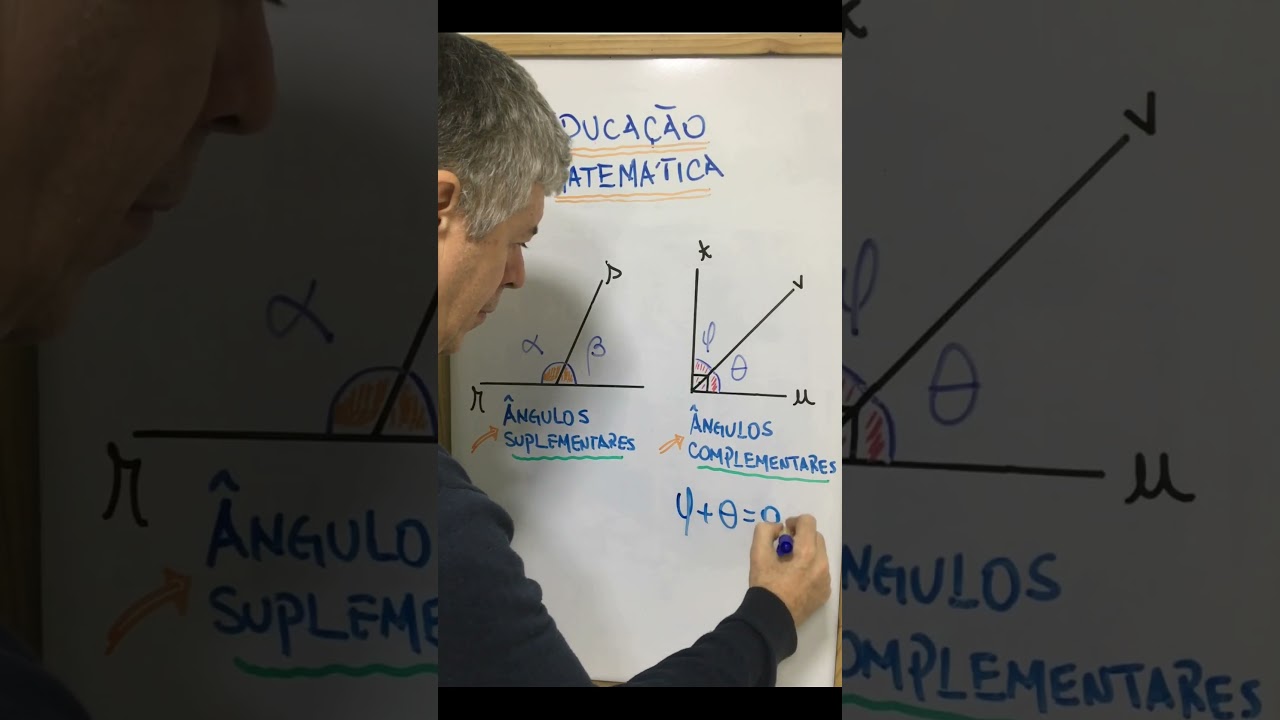
Ângulos Complementares e Suplementares

Introdução

Dois ângulos são chamados de complementares quando a soma deles resulta em 90 graus. Já os ângulos são ditos suplementares quando a soma deles totaliza 180 graus. Entender esses conceitos é fundamental para a resolução de problemas envolvendo medidas de ângulos.

Ângulos Complementares

Ângulos complementares são aqueles que, quando somados, resultam em um ângulo reto, ou seja, 90 graus. Por exemplo, se um ângulo mede 30 graus, o seu complementar será de 60 graus, pois 30 + 60 = 90 graus.

Ângulos Suplementares

Já os ângulos suplementares são aqueles que, somados, resultam em uma reta completa, totalizando 180 graus. Por exemplo, se um ângulo mede 100 graus, o seu suplementar será de 80 graus, pois 100 + 80 = 180 graus.

Conclusão

Compreender a relação entre ângulos complementares e suplementares é essencial para resolver problemas de geometria e trigonometria. Lembre-se sempre que a soma dos ângulos complementares é 90 graus, enquanto a soma dos ângulos suplementares é 180 graus.

Angulos complementares e suplementares: o que são e como identificá-los

O que são ângulos complementares?

Os ângulos complementares são dois ângulos cuja soma é igual a 90 graus. Ou seja, quando dois ângulos complementares são somados, o resultado é um ângulo reto. Por exemplo, se um ângulo mede 30 graus, seu complementar será de 60 graus.

Para identificar dois ângulos complementares, basta somá-los e verificar se o resultado é igual a 90 graus. Caso afirmativo, os ângulos são complementares.

Exemplo de ângulos complementares

Vamos considerar dois ângulos A e B. Se A mede 45 graus, então B será seu complementar e terá a medida de 45 graus, já que 45 + 45 = 90 graus. Nesse caso, podemos afirmar que os ângulos A e B são complementares.

Outro exemplo seria se um ângulo medisse 20 graus. Seu complementar teria que medir 70 graus, pois 20 + 70 = 90 graus, formando assim um ângulo reto.

Por isso, os ângulos complementares são fundamentais para resolver problemas matemáticos e geometria.

O que são ângulos suplementares?

Diferentemente dos complementares, os ângulos suplementares são dois ângulos cuja soma é igual a 180 graus. Ou seja, quando somados, formam uma linha reta.

Para identificar dois ângulos suplementares, basta somá-los e verificar se o resultado é igual a 180 graus. Se isso ocorrer, os ângulos são considerados suplementares.

Exemplo de ângulos suplementares

Imagine dois ângulos C e D. Se C mede 120 graus, então seu ângulo suplementar D terá 60 graus, pois 120 + 60 = 180 graus. Dessa forma, podemos concluir que os ângulos C e D são suplementares.

Outro exemplo seria se um ângulo medisse 45 graus. Seu ângulo suplementar teria que medir 135 graus, pois 45 + 135 = 180 graus, formando assim uma linha reta.

Portanto, os ângulos complementares e suplementares são essenciais para resolver problemas de matemática e geometria, sendo importantes conceitos a serem dominados.

Importância dos ângulos complementares e suplementares na matemática

Os ângulos complementares e suplementares são conceitos fundamentais na matemática que ajudam a compreender as relações entre diferentes medidas de ângulos. Compreender essas relações é essencial para resolver problemas geométricos e trigonométricos, além de ser um conhecimento fundamental para diversas áreas da ciência e engenharia.

Aplicações práticas dos ângulos complementares e suplementares

Na prática, os ângulos complementares somam 90 graus, enquanto os suplementares somam 180 graus. Essas relações são úteis em diversas situações do cotidiano, como na construção civil, na indústria de manufatura e até mesmo em jogos digitais que simulam ambientes tridimensionais. Compreender a matemática por trás desses conceitos pode abrir portas para uma maior compreensão do mundo ao nosso redor.

Estímulo ao aprendizado de ângulos complementares e suplementares nas escolas

É fundamental que as escolas incentivem o aprendizado dos conceitos de ângulos complementares e suplementares desde cedo, pois isso pode contribuir para o desenvolvimento do raciocínio lógico, da capacidade de resolver problemas complexos e da criatividade dos estudantes. Além disso, compreender esses conceitos pode melhorar o desempenho em disciplinas como matemática e física, preparando os alunos para desafios futuros.

Importância do conhecimento de ângulos complementares e suplementares na formação educacional

Os ângulos complementares e suplementares desempenham um papel fundamental no aprendizado da matemática e em diversas áreas do conhecimento. Compreender esses conceitos não só amplia a capacidade de resolver problemas, mas também estimula o desenvolvimento de habilidades essenciais para o sucesso acadêmico e profissional. Portanto, é crucial que escolas e educadores valorizem o ensino e a prática de ângulos complementares e suplementares, garantindo que os estudantes estejam preparados para enfrentar os desafios do mundo moderno.

Fonte Consultada: Texto gerado a partir do Vídeo https://www.youtube.com/watch?v=snG2YpRJ6tM do Canal Supermática - Física e Matemática .