Introdução

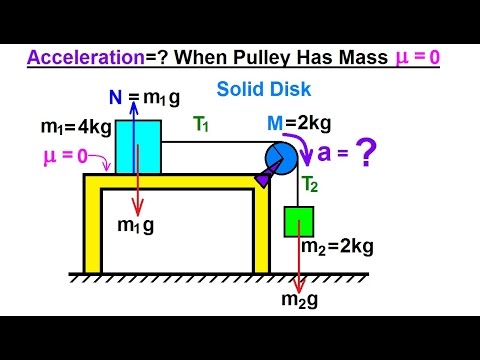
Bem-vindo ao Electron Line! Neste exemplo, vamos encontrar a aceleração do sistema. Parece um pouco com a aplicação da segunda lei de Newton, mas com uma grande diferença: a polia tem massa e, portanto, momento de inércia, o que afetará a aceleração do sistema. Além disso, mesmo havendo uma única corda conectando duas massas m1 e m2, a tensão deste lado da corda, chamada de t1, não será igual à tensão do outro lado da corda, chamada de t2, devido à presença da polia com massa e momento de inércia. Isso resultará em várias equações para resolver o problema.

Desenvolvimento

A primeira equação será o torque na polia igual ao momento de inércia da polia multiplicado pela aceleração angular. Além disso, teremos duas equações relacionando força (F) com massa (M) e aceleração (A) para as duas massas do sistema. As equações resultarão em três incógnitas: t2, t1 e a aceleração do sistema.

No primeiro bloco, o torque causado pela diferença de tensão entre t2 e t1 resulta na equação t2 – t1 = 1/2 massa da polia aceleração linear.

A segunda equação relaciona as forças atuando na massa m2: m2g – t2 = m2 aceleração. Por fim, a terceira equação relaciona as forças na massa m1: t1 = m1 aceleração.

Resolvendo as equações para t2 e t1 e substituindo-as na equação do torque, eliminamos as incógnitas e obtemos a equação final apenas com a aceleração como desconhecida.

Calculando a Aciação

Dado os valores das massas envolvidas, calculamos a aceleração como a = 2 / (2 + 4 + 1/2) G. Assim, a aceleração do sistema é igual a 2 / 7 G.

Este é o processo utilizado para encontrar a aceleração de um sistema com uma polia que possui massa e, consequentemente, momento de inércia, em uma situação onde não há atrito entre o bloco e a mesa.

Aplicação do Momento de Inércia (6 de 11) – Aceleração quando a Polia tem massa (μ=0)

Introdução

Neste artigo, abordaremos a aplicação do momento de inércia em um cenário onde a polia possui massa. A questão em destaque é calcular a aceleração do sistema quando a polia está em movimento.

O que é momento de inércia?

O momento de inércia é uma grandeza física que mede a resistência que um corpo oferece à variação de sua velocidade angular. Ele depende da distribuição de massa do objeto e do eixo de rotação.

Fórmula para calcular aceleração

Para determinar a aceleração do sistema quando a polia possui massa, precisamos levar em consideração a equação que relaciona momento de inércia, força e aceleração.

Fórmula do momento de inércia

A fórmula para o cálculo do momento de inércia de um objeto depende da sua forma geométrica e distribuição de massa. Para uma polia com massa, é preciso considerar a contribuição da própria polia para o momento de inércia do sistema.

Métodos de resolução

Existem diferentes métodos para resolver problemas envolvendo momento de inércia, como a aplicação de equações de movimento e princípios da dinâmica. É importante fazer uma análise completa do sistema para determinar a aceleração correta.

Exemplo numérico

Vamos considerar um exemplo numérico para ilustrar o cálculo da aceleração quando a polia tem massa. Utilizaremos os dados fornecidos no enunciado do problema para encontrar a solução.

Análise do problema

Para resolver este tipo de situação, é fundamental considerar todos os aspectos do sistema, incluindo a massa da polia e sua contribuição para a aceleração total. É essencial realizar os cálculos de forma precisa e cuidadosa.

Conclusão

Neste artigo, exploramos a aplicação do momento de inércia em um cenário específico, onde a polia possui massa. Através da análise cuidadosa do problema e da aplicação correta das fórmulas, foi possível determinar a aceleração do sistema. É importante compreender os princípios fundamentais da física para resolver questões desafiadoras como essa.

A importância da educação em física

A física é uma disciplina fundamental para o entendimento do mundo ao nosso redor, sendo essencial para o desenvolvimento tecnológico e científico. O estudo da física proporciona um conhecimento profundo sobre os fenômenos naturais, permitindo a aplicação de conceitos teóricos em situações práticas, como no cálculo da aceleração em sistemas complexos, como no momento de inércia de polias com massa.

A importância da prática na aprendizagem em física

Para compreender os conceitos físicos de forma mais efetiva, é essencial a realização de experimentos e práticas. A aplicação dos conhecimentos teóricos em situações reais, como no cálculo da aceleração em polias com massa, proporciona uma maior fixação do conteúdo e um melhor entendimento dos fenômenos estudados. Além disso, a prática estimula o desenvolvimento do pensamento crítico e da resolução de problemas.

O papel do professor na educação em física

O professor de física desempenha um papel fundamental na formação dos estudantes, sendo responsável por transmitir o conhecimento de forma clara e estimulante. Através de uma abordagem inovadora e dinâmica, o professor pode despertar o interesse dos alunos pela disciplina, incentivando a busca pelo conhecimento e o desenvolvimento do raciocínio lógico. Dessa forma, a educação em física se torna um processo enriquecedor e motivador para os estudantes, preparando-os para os desafios do mundo contemporâneo.

Importância da educação em física: compreendendo os fenômenos naturais através da prática e do ensino efetivo

Fonte Consultada: Texto gerado a partir do Vídeo https://www.youtube.com/watch?v=qu46xL4KPvU do Canal Michel van Biezen .