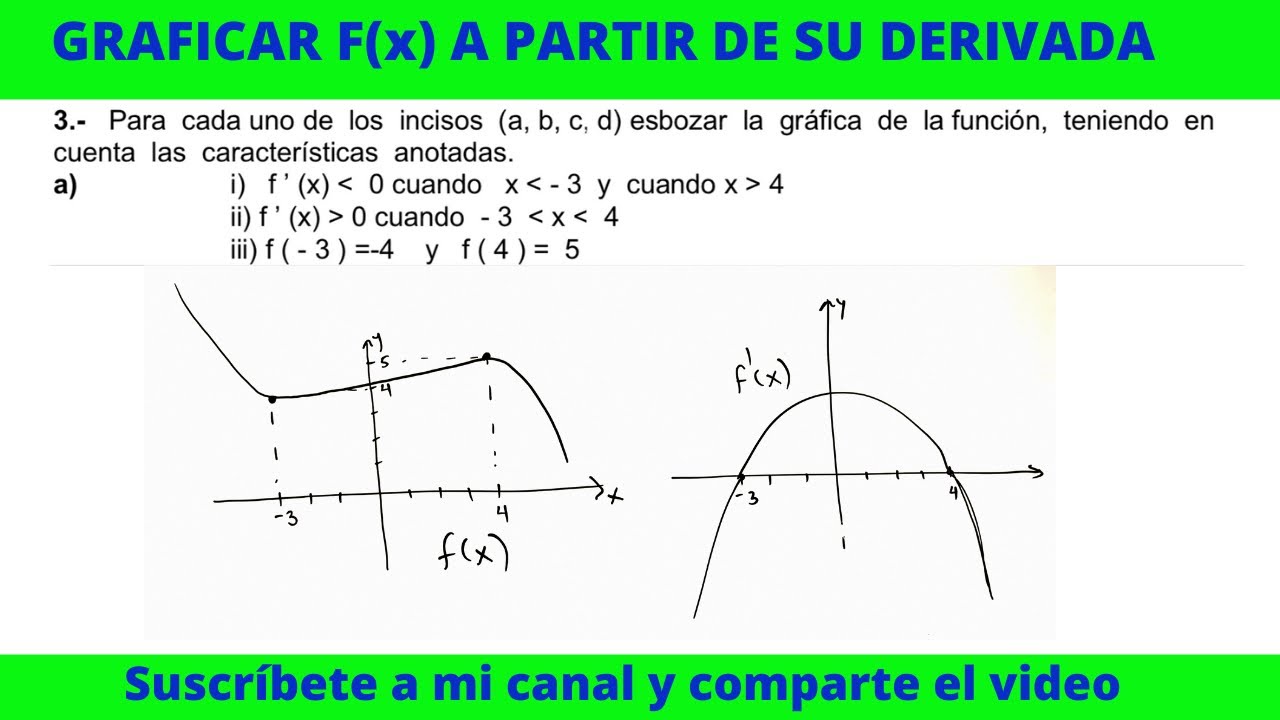
Gráfico de uma função a partir de sua derivada e condições.
Introdução
Neste exercício, foi solicitado que fosse feito o gráfico da função utilizando as condições fornecidas sobre a derivada da função. A derivada deve ser negativa quando x é menor que -3 e maior que 4, e positiva quando x está entre -3 e 4. Além disso, os pontos onde a derivada é igual a 0 correspondem aos mínimos e máximos da função original.
Graficando a função
Para representar graficamente essas condições, é necessário entender como a derivada afeta o comportamento da função. Quando a derivada é negativa, a função está decrescente, e quando a derivada é positiva, a função está crescente. Com base nisso, é possível representar a função de acordo com as restrições especificadas.
A função f(-3) é igual a X, f(4) é igual a 5, esses pontos correspondem aos mínimos e máximos da função. É importante lembrar como esses pontos são afetados pela derivada.
Conclusão
Ao seguir as condições fornecidas sobre a derivada da função, foi possível criar um gráfico que representa adequadamente o comportamento da função. É fundamental entender como a derivada influencia a função e como isso é refletido no gráfico final.
Análise Gráfica a Partir da Derivada e Condições
Introdução
Ao estudar funções matemáticas, uma das ferramentas mais poderosas é a derivada. A partir dela, podemos não apenas determinar a taxa de variação de uma função, mas também obter informações sobre a forma do gráfico da função original. Neste artigo, vamos explorar como graficar uma função a partir de sua derivada e de algumas condições específicas.
O Que é a Derivada de uma Função?
Antes de prosseguirmos, é importante revisar o conceito de derivada. Em termos simples, a derivada de uma função é a taxa de variação instantânea dessa função em um determinado ponto. Graficamente, a derivada nos dá a inclinação da reta tangente à curva da função nesse ponto.
Graficando uma Função a Partir de sua Derivada
Para graficar uma função a partir de sua derivada, devemos proceder da seguinte maneira:
- Passo 1: Obter a derivada da função original
- Passo 2: Identificar os pontos críticos onde a derivada se anula ou é indefinida
- Passo 3: Determinar o comportamento da função nos intervalos definidos pelos pontos críticos
- Passo 4: Utilizar as informações obtidas para esboçar o gráfico da função
Condições para Graficar uma Função a Partir de sua Derivada
Além de utilizar a derivada, algumas condições específicas podem nos ajudar a compor o gráfico da função original. Algumas dessas condições são:
- Condição de Monotonicidade: Se a derivada for sempre positiva em um intervalo, a função original é crescente nesse intervalo. Da mesma forma, se a derivada for sempre negativa, a função é decrescente.
- Condição de Concavidade: A segunda derivada nos fornece informações sobre a concavidade da função original. Se a segunda derivada for positiva, a função é côncava para cima, e se for negativa, a função é côncava para baixo.
Exemplo Prático
Para ilustrar o processo de graficar uma função a partir de sua derivada, consideremos a função ( f(x) = x^3 - 3x^2 + 2x ). Vamos seguir os passos mencionados anteriormente e utilizar as condições de monotonicidade e concavidade para obter o gráfico completo da função.
Conclusão
Neste artigo, exploramos o processo de graficar uma função a partir de sua derivada e de algumas condições específicas. Entender como a derivada e essas condições influenciam o comportamento da função nos permite visualizar de forma mais clara o seu gráfico. Esperamos que esse conhecimento seja útil em seus estudos e aplicações práticas.
Análise de gráficos de funções a partir da sua derivada e condições
Ao analisar o gráfico de uma função a partir da sua derivada, é possível identificar pontos críticos como máximos, mínimos e pontos de inflexão. Utilizando as condições de primeira e segunda derivada, é possível determinar o comportamento da função em diferentes intervalos, contribuindo para uma compreensão mais precisa do seu comportamento global.
Interpretação dos resultados obtidos na análise de gráficos
Após a identificação dos pontos críticos e do comportamento da função nos diferentes intervalos, é possível interpretar os resultados obtidos e traçar conclusões sobre o comportamento da função. A análise do gráfico a partir da sua derivada e condições permite uma compreensão mais profunda do comportamento da função e das relações entre suas diferentes partes.
Aplicação prática na educação e solução de problemas matemáticos
A análise de gráficos a partir da derivada e condições é uma ferramenta fundamental na educação matemática, permitindo aos estudantes compreenderem o comportamento das funções de maneira mais intuitiva e visual. Além disso, essa abordagem facilita a resolução de problemas matemáticos complexos, auxiliando no desenvolvimento do raciocínio lógico e na aplicação de conceitos matemáticos em diversas situações práticas.
Conclusão sobre a importância da análise de gráficos a partir da derivada e condições
Em suma, a análise de gráficos a partir da derivada e condições é uma ferramenta essencial para a compreensão do comportamento das funções e para a resolução de problemas matemáticos. Essa abordagem permite uma interpretação mais precisa dos resultados obtidos, contribuindo para o desenvolvimento das habilidades matemáticas dos estudantes e para a aplicação prática dos conceitos aprendidos em sala de aula.
Fonte Consultada: Texto gerado a partir do Vídeo https://www.youtube.com/watch?v=vumSngWughs do Canal Profe Santiago Velasquez .