Introdução
Adição, multiplicação, composição de função, adição modular, multiplicação de matriz, leis de grupo, e operações lógicas como “e” e “ou”, concatenção e até o maior divisor comum são todas operações associativas. Existe algo que as liga? A resposta é surpreendente e tem implicações profundas. Ao final deste vídeo, você entenderá que associatividade não é apenas uma propriedade, mas sim uma ideia.
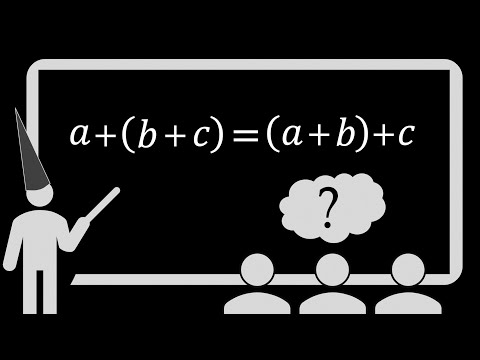
Você provavelmente aprendeu pela primeira vez sobre a propriedade associativa na escola primária. Quando aprendeu, provavelmente lhe disseram que associatividade é uma regra escrita assim para adição e assim para multiplicação, que você deveria aprender a associatividade para fazer cálculos aritméticos. Associatividade significa que a ordem das operações não importa e, como tal, onde os parênteses vão não importa. Foi provavelmente ensinado ao lado da comutatividade e talvez você até se lembre de qual é qual.
Se isso soa como você, quero que saiba que suas ideias sobre a propriedade associativa foram corrompidas, mas não se preocupe, não é culpa sua, nem do seu professor. O fato é que seu professor não sabia melhor. Quando foi a última vez que você usou a propriedade associativa em um cálculo aritmético? Pense em como você resolveria essa equação. Provavelmente usaria um truque muito mais inteligente para navegar pela aritmética, o que chamarei de propriedade de “misturar”, que é verdade para operações que são tanto associativas quanto comutativas.
Associatividade
Seguindo por esse caminho, a curiosidade sobre a propriedade associativa é praticamente inexistente, o que é uma pena, pois acredito que é a propriedade mais poderosa das operações e uma vez que você a entenda, acredito que concordará. Um desafio revelador é tentar explicar a alguém o que é uma operação associativa sem simplesmente descrever a propriedade formal em palavras. Para tornar o desafio mais concreto, evite ler a equação e tente evitar usar as palavras parênteses, ordem, grupo e seus sinônimos.
Agora que sabemos como a associatividade é tipicamente explicada e qual é a sua definição, o que associatividade nos diz sobre as operações? Para descobrir, vamos começar olhando para um punhado de operações associativas, começando pela adição. Suponha que em uma tigela eu tenha duas maçãs e em outra tigela eu tenha três maçãs. Gostaria de combinar as maçãs das duas tigelas. Se eu fizer isso e depois contar o número de maçãs, descobrirei que tenho cinco maçãs. Matematicamente, essa observação é escrita como dois mais três é igual a cinco e significa duas coisas, e mais três coisas fazem cinco coisas.
Matemática e Operações Associativas
O texto descreve a importância da associatividade em várias operações matemáticas e como essa propriedade pode ser interpretada de diferentes maneiras, como ação/objeto, gluing, entre outros. A essência é que a associatividade é fundamental nas operações e sua compreensão pode revolucionar a forma como entendemos e utilizamos operações matemáticas. Cada exemplo dado demonstra como a associatividade está presente em diferentes contextos, levando o leitor a uma compreensão mais profunda dessa propriedade matemática. A maneira como as operações são associadas e como podem ser interpretadas de formas distintas mostra a versatilidade e a complexidade da associatividade. Ao final, o autor destaca a importância da associatividade em áreas como grupos matemáticos, reforçando a ideia de que se trata de uma propriedade essencial em diversos campos da matemática.
A Propriedade Associativa: A Equação mais Mal-Compreendida na Matemática
Introdução
A propriedade associativa é um conceito fundamental na matemática que desempenha um papel crucial em diversas operações matemáticas. No entanto, muitas pessoas encontram dificuldades em compreender e aplicar essa propriedade corretamente. Neste artigo, vamos explorar em detalhes a propriedade associativa, desmistificando-a e fornecendo exemplos práticos para facilitar o entendimento.
O que é a Propriedade Associativa?
A propriedade associativa é uma das propriedades básicas das operações matemáticas, como adição e multiplicação. Essa propriedade afirma que a forma como os elementos são agrupados em uma operação não afeta o resultado final. Em termos simples, isso significa que a ordem em que as operações são realizadas não altera o resultado final.
Como Funciona na Prática
Para entender melhor a propriedade associativa, vamos considerar um exemplo com a adição. Suponha que temos três números: 2, 3 e 4. Se quisermos somar esses números, podemos fazer de duas maneiras diferentes:
Forma Tradicional
2 + 3 + 4 = 9
Utilizando a Propriedade Associativa
(2 + 3) + 4 = 5 + 4 = 9
2 + (3 + 4) = 2 + 7 = 9
Como podemos ver, o resultado final é o mesmo, independentemente da forma como agrupamos os números para realizar a adição. Isso é possível graças à propriedade associativa.
Importância da Propriedade Associativa
A propriedade associativa é essencial na matemática, pois simplifica cálculos e facilita a resolução de problemas. Ao compreender e aplicar corretamente essa propriedade, é possível tornar operações matemáticas mais eficientes e precisas.
Além disso, a propriedade associativa é amplamente utilizada em várias áreas da matemática, como álgebra, trigonometria e cálculo. Dominar esse conceito é fundamental para o sucesso em disciplinas matemáticas mais avançadas.
Exemplos Adicionais
Para reforçar ainda mais a compreensão da propriedade associativa, vamos analisar mais alguns exemplos com diferentes operações matemáticas:
Multiplicação
(A x B) x C = A x (B x C)
Subtração
(A – B) – C = A – (B – C)
Conclusão
A propriedade associativa é um conceito essencial na matemática que muitas vezes é mal-interpretado. Compreender como essa propriedade funciona e aplicá-la corretamente pode simplificar cálculos e facilitar a resolução de problemas matemáticos. Ao dominar a propriedade associativa, os estudantes podem melhorar sua proficiência em matemática e obter sucesso em disciplinas mais avançadas.
O Papel da Propriedade Associativa na Educação Matemática
A propriedade associativa é uma das propriedades fundamentais da matemática que nem sempre é compreendida pelos alunos. Através do uso de exemplos e exercícios práticos, os educadores podem ajudar os estudantes a entender como essa propriedade funciona e como ela pode simplificar cálculos matemáticos complexos.
A Importância de Ensinar a Propriedade Associativa de Forma Eficaz
Quando os alunos compreendem a propriedade associativa, eles são capazes de resolver problemas de matemática mais rapidamente e com mais confiança. Além disso, a habilidade de aplicar essa propriedade em diferentes contextos matemáticos pode ajudar os estudantes a desenvolver habilidades de pensamento crítico e resolução de problemas.
Desafios e Oportunidades na Educação Matemática em Relação à Propriedade Associativa
Apesar de ser uma ferramenta poderosa na resolução de problemas matemáticos, a propriedade associativa muitas vezes é mal compreendida pelos alunos. Os educadores enfrentam o desafio de encontrar maneiras criativas e eficazes de ensinar essa propriedade, a fim de melhorar a compreensão e o desempenho dos estudantes em matemática. Com o uso de recursos educacionais inovadores e estratégias de ensino diferenciadas, os educadores podem ajudar os alunos a dominar a propriedade associativa e aprimorar suas habilidades matemáticas.
Conclusão
A propriedade associativa é uma ferramenta essencial para a resolução de problemas matemáticos e seu ensino eficaz pode melhorar significativamente o desempenho dos alunos. Educadores devem buscar maneiras inovadoras de ensinar essa propriedade, tornando-a acessível e relevante para os estudantes. Através da aplicação prática da propriedade associativa em diferentes contextos matemáticos, os alunos podem desenvolver habilidades de pensamento crítico e resolução de problemas que serão valiosas ao longo de suas vidas acadêmicas e profissionais.
Fonte Consultada: Texto gerado a partir do Vídeo https://www.youtube.com/watch?v=Oq71Ev9-aQE do Canal Lingua Mathematica .