Introdução

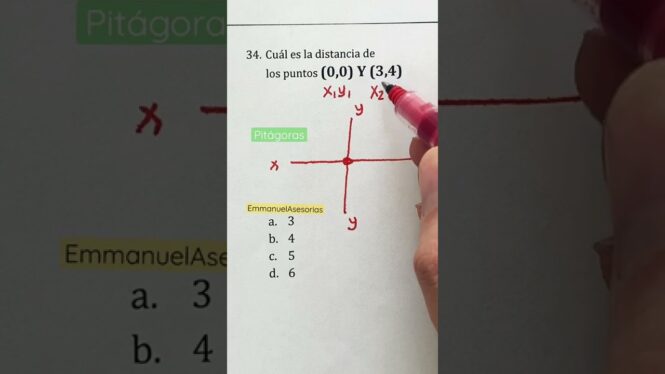
Vamos calcular a distância entre os pontos (0,0) e (3,4) no plano cartesiano.

Método de cálculo

Para encontrar a distância entre esses dois pontos, podemos usar o teorema de Pitágoras, já que formam um triângulo retângulo. A altura do triângulo é 4 (diferença entre as coordenadas y) e a base é 3 (diferença entre as coordenadas x).

Cálculo da distância

Então, aplicando o teorema de Pitágoras, temos que:

D = √(3² + 4²)

D = √(9 + 16)

D = √25

D = 5

Portanto, a distância entre os pontos (0,0) e (3,4) é 5 unidades.

Cálculo da distância entre dois pontos utilizando o Teorema de Pitágoras

Quando precisamos encontrar a distância entre dois pontos em um plano cartesiano, o Teorema de Pitágoras se revela uma ferramenta extremamente útil. Neste artigo, vamos explorar como utilizar esse teorema para calcular distâncias, considerando a hipotenusa e os catetos envolvidos no processo. Continue lendo e aprenda como aplicar esse conhecimento de maneira prática.

O que é o Teorema de Pitágoras?

O Teorema de Pitágoras é uma das mais famosas proposições matemáticas e estabelece a relação entre os lados de um triângulo retângulo. Em termos simples, o teorema afirma que a soma dos quadrados dos catetos de um triângulo retângulo é igual ao quadrado da hipotenusa. Matematicamente, podemos representar o teorema da seguinte forma: a² + b² = c², onde "a" e "b" são os catetos e "c" é a hipotenusa.

Como calcular a distância entre dois pontos?

Para calcular a distância entre dois pontos em um plano cartesiano, podemos utilizar o Teorema de Pitágoras. Suponha que temos dois pontos A(x₁, y₁) e B(x₂, y₂). A distância entre esses dois pontos pode ser encontrada aplicando a fórmula:

[
d = sqrt{((x₂ – x₁)² + (y₂ – y₁)²)}
]

Nessa fórmula, a distância "d" corresponde à hipotenusa do triângulo retângulo formado pelos catetos (x₂ – x₁) e (y₂ – y₁). Para facilitar o cálculo, podemos simplificar a expressão da seguinte maneira:

[
d = sqrt{(Δx)² + (Δy)²}
]

Onde Δx = x₂ – x₁ e Δy = y₂ – y₁.

Exemplo prático

Para exemplificar o cálculo da distância entre dois pontos, considere os pontos A(1, 2) e B(4, 6). Primeiramente, devemos calcular os deltas Δx e Δy:

Δx = 4 – 1 = 3

Δy = 6 – 2 = 4

Em seguida, substituímos os valores na fórmula da distância:

[
d = sqrt{(3)² + (4)²}
]
[
d = sqrt{9 + 16}
]
[
d = sqrt{25}
]
[
d = 5
]

Portanto, a distância entre os pontos A(1, 2) e B(4, 6) é igual a 5 unidades.

Conclusão

O Teorema de Pitágoras é uma ferramenta fundamental para o cálculo da distância entre dois pontos em um plano cartesiano. Ao compreender e aplicar essa proposição matemática, torna-se mais simples resolver problemas que envolvam a determinação de distâncias. Pratique o uso do Teorema de Pitágoras em diferentes contextos e aprimore suas habilidades matemáticas. Agora que você conhece essa técnica, não deixe de utilizá-la em suas futuras atividades envolvendo geometria e trigonometria.

Teorema de Pitágoras na Educação

O Teorema de Pitágoras é um dos conceitos fundamentais na matemática e desempenha um papel importante na educação, principalmente no ensino de geometria. Ao estudar a relação entre os catetos e a hipotenusa de um triângulo retângulo, os alunos podem desenvolver habilidades de raciocínio lógico e aplicar conceitos matemáticos na resolução de problemas.

Aplicação do Teorema de Pitágoras

Além de ser uma ferramenta essencial no estudo da geometria, o Teorema de Pitágoras também possui diversas aplicações práticas em áreas como a engenharia, arquitetura e geografia. Calcular a distância entre dois pontos em um plano cartesiano, por exemplo, envolve o uso do Teorema de Pitágoras para determinar a hipotenusa do triângulo formado pelos pontos e seus respectivos catetos.

Importância do Ensino de Matemática

O ensino do Teorema de Pitágoras e de outros conceitos matemáticos é essencial para o desenvolvimento intelectual dos estudantes, pois estimula o pensamento crítico, a resolução de problemas e a capacidade de abstração. Portanto, é fundamental que as escolas incentivem o aprendizado da matemática de forma criativa e dinâmica, possibilitando aos alunos a aplicação dos conhecimentos adquiridos em situações do cotidiano.

Relevância do Teorema de Pitágoras na Educação

O Teorema de Pitágoras representa não apenas um conceito matemático, mas também uma ferramenta fundamental para o desenvolvimento cognitivo dos estudantes. Ao entender e aplicar esse teorema, os alunos não apenas fortalecem suas habilidades matemáticas, mas também ampliam seu repertório de conhecimentos e habilidades para enfrentar desafios acadêmicos e profissionais futuros. Portanto, é imprescindível que o ensino da matemática seja valorizado e incentivado como parte essencial da formação educacional.

Fonte Consultada: Texto gerado a partir do Vídeo https://www.youtube.com/watch?v=QClL08Pf088 do Canal EMMANUEL ASESORÍAS .